PERSAMAAN LINGKARAN KELAS XI SMA

PERSAMAAN LINGKARAN

  Hallo teman-teman, selamat datang di blog kami dari SMA NEGERI 1 UNAAHA. blog ini disusun oleh Dhifa Faradiyah dan Widya Ayuning Paramitha dari kelompok 4 kelas XI MIPA 3. disini kami akan berbagi pengetahuan mengenai MATERI MATEMATIKA PEMINATAN "PERSAMAAN LINGKARAN" mulai dari peta konsep,sejarah, definisi, rumus, turunan hingga aplikasi dalam kehidupan sehari-hari . berikut ulasannya😊

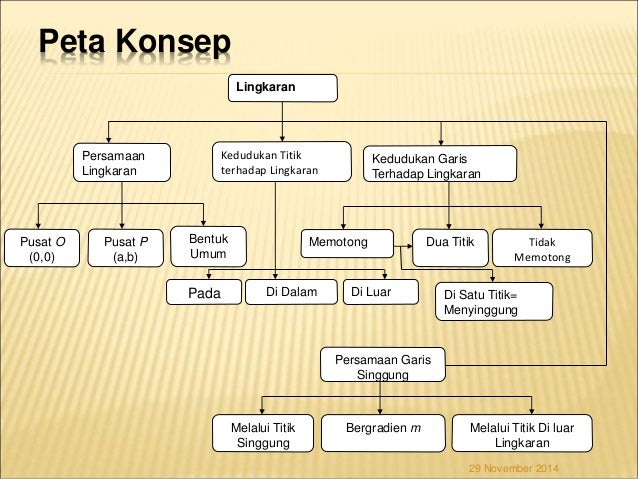
1.PETA KONSEP


  

2. SEJARAH LINGKARAN 

A. ASAL USUL

Lingkaran sudah ada sejak jaman prasejarah. Penemuan roda adalah penemuan mendasar dari sifat lingkaran. Orang-orang Yunani menganggap Mesir sebagai penemu geometri. Juru tulis Ahmes, penulis dari papirus Rhind, memberikan aturan untuk menentukan area dari sebuah lingkaran yang sesuai dengan π = 256 / 81 atau sekitar 3,16.

Teorema pertama yang berhubungan dengan lingkaran yang dikaitkan dengan Thales sekitar 650 SM. Buku III dari Euclid 's Elements berurusan dengan sifat lingkaran dan masalah inscribing dan escribing poligon.

Salah satu masalah matematika Yunani adalah masalah menemukan persegi dengan wilayah yang sama sebagai sebuah lingkaran yang diberikan. Beberapa 'kurva terkenal dalam tumpukan pertama kali dipelajari dalam upaya untuk memecahkan masalah ini. Anaxagoras di 450 SM adalah matematikawan recored pertama untuk studi masalah ini.

Masalah untuk menemukan luas lingkaran menyebabkan integrasi. Untuk lingkaran dengan rumus yang diberikan di atas wilayah ini π^2 dan panjang kurva adalah suatu 2π.
Pedal lingkaran adalah cardioid jika titik pedal diambil pada lingkar dan merupakan limacon jika titik pedal bukan pada keliling.

kaustik dari sebuah lingkaran dengan titik bersinar di keliling adalah cardioid, sedangkan bila sinar sejajar maka kaustik adalah nephroid .

Apollonius, pada sekitar 240 SM, efektif menunjukkan bahwa persamaan r bipolar = kr 'merupakan sistem lingkaran koaksial sebagai k bervariasi. Dalam hal persamaan bipolar mr^2 + nr^2 = c^2 merupakan sebuah lingkaran yang pusatnya membagi ruas garis antara dua titik tetap dari sistem dalam rasio n ke m.


B.PENEMU


Zu Chongzhi

Dalam sejarah Tiongkok banyak ahli matematika berupaya menghitung π. Sedangkan hasil ya ng dicapai Zu Chongzhi pada abad ke-5 dapat dikatakan merupakan kemajuan dalam penghitungan π. Zu Chongzhi lahir di kota Jiankang( kota Nanjing) pada tahun 429. sejak kecil ia sangat cerdas dan suka pengetahuan di bidang matematika dan astronomi. Pada tahun 464 ketiga ia berumur 35 tahun, Zu Chengzhi mulai menghitung π.

Dalam kehidupan sehari-hari rakyat Tiongkok mengetahui bahwa panjang keliling lingkaran sama dengan tiga kali libat lebih diameter lingkaran. Sebelum Zu Chongzhi, ahli matematika Tiongkok Liu Hui mengajukan cara ilmia untuk menghitungkan π, dengan panjang keliling regular polygon dalam lingkaran untuk mendekati panjang keliling lingkaran yang asli. Dengan cara ini Liu Hui telah menghitungkan π sampai 4 angka dibelakang koma. Sedangkan melalui penelitian Zu Chongzhi, π telah dihitungkan sampai 7 angka di belakang koma yaitu diantara 3.1415926 dengan 3.1415927, dan memperoleh nilai mirip π dalam bentuk bilangan pecahan.

Untuk memperingati hasil Zu Chongzhi, ahli sejarah matematika di luar negeri pernah mengusulkan menamakan π dengan tingkat Zu. Zu Chongzhi dan anaknya juga menyelesaikan penghitungan volume bola. Prinsip matematika itu dinamakan prinsip Zu. 

Sebelum abad ke-14, Tiongkok adalah negara yang relatif maju dalam bidang matematika.

 

Rene Descartes

Di desa La Haye-lah tahun 1596 lahir jabang bayi Rene Descartes, filosof, ilmuwan, matematikus Perancis yang tersohor. Waktu mudanya dia sekolah Yesuit, College La Fleche. Begitu umur dua puluh dia dapat gelar ahli hukum dari Universitas Poitiers walau tidak pernah mempraktekkan ilmunya samasekali. Meskipun Descartes peroleh pendidikan baik, tetapi dia yakin betul tak ada ilmu apa pun yang bisa dipercaya tanpa matematik. Karena itu, bukannya dia meneruskan pendidikan formalnya, melainkan ambil keputusan kelana keliling Eropa dan melihat dunia dengan mata kepala sendiri. Berkat dasarnya berasal dari keluarga berada, mungkinlah dia mengembara kian kemari dengan leluasa dan longgar. Tak ada persoalan duit. 

Dari tahun 1616 hingga 1628, Descartes betul-betul melompat ke sana kemari, dari satu negeri ke negeri lain. Dia masuk tiga dinas ketentaraan yang berbeda-beda (Belanda, Bavaria dan Honggaria), walaupun tampaknya dia tidak pernah ikut bertempur samasekali. Dikunjungi pula Italia, Polandia, Denmark dan negeri-negeri lainnya. Dalam tahun-tahun ini, dia menghimpun apa saja yang dianggapnya merupakan metode umum untuk menemukan kebenaran. Ketika umurnya tiga puluh dua tahun, Descartes memutuskan menggunakan metodenya dalam suatu percobaan membangun gambaran dunia yang sesungguhnya. Dia lantas menetap di Negeri Belanda dan tinggal di sana selama tidak kurang dari dua puluh satu tahun. (Dipilihnya Negeri Belanda karena negeri itu dianggapnya menyediakan kebebasan intelektual yang lebih besar ketimbang lain-lain negeri, dan karena dia ingin menjauhkan diri dari Paris yang kehidupan sosialnya tidak memberikan ketenangan cukup). 

Sekitar tahun 1629 ditulisnya Rules for the Direction of the Mind buku yang memberikan garis-garis besar metodenya. Tetapi, buku ini tidak komplit dan tampaknya ia tidak berniat menerbitkannya. Diterbitkan untuk pertama kalinya lebih dari lima puluh tahun sesudah Descartes tiada. Dari tahun 1630 sampai 1634, Descartes menggunakan metodenya dalam penelitian ilmiah. Untuk mempelajari lebih mendalam tentang anatomi dan fisiologi, dia melakukan penjajagan secara terpisah-pisah. Dia bergumul dalam bidang-bidang yang berdiri sendiri seperti optik, meteorologi, matematik dan pelbagai cabang ilmu lainnya. 

Menjadi keinginan Descartes sendiri mempersembahkan hasil-hasil penyelidikan ilmiahnya dalam buku yang disebut Le Monde (Dunia). Tetapi, di tahun 1633, tatkala buku itu hampir rampung, dia dengan penguasa gereja di Italia mengutuk Galileo karena menyokong teori Copernicus bahwa dunia ini sebenarnya bulat, bukannya datar, dan bumi itu berputar mengitari matahari, bukan sebaliknya. Meskipun di Negeri Belanda dia tidak berada di bawah kekuasaan gereja Katolik, toh dia berkeputusan berhati-hati untuk tidak menerbitkan bukunya walau dia pun sebenarnya sepakat dengan teori Copernicus. Sebagai gantinya, di tahun 1637 dia menerbitkan bukunya yang masyhur Discourse on the Method for Properly Guiding the Reason and Finding Truth in the Sciences (biasanya diringkas saja Discourse on Method). 

Discourse ditulis dalam bahasa Perancis dan bukan Latin sehingga semua kalangan intelegensia dapat membacanya, termasuk mereka yang tak peroleh pendidikan klasik. Sebagai tambahan Discourse ada tiga esai. 

Didalamnya Descartes menyuguhkan contoh-contoh penemuan-penemuan yang telah dilakukannya dengan menggunakan metode itu. Tambahan pertamanya Optics, Descartes menjelaskan hukum pelengkungan cahaya (yang sesungguhnya sudah ditemukan oleh Willebord Snell). Dia juga mempersoalkan masalah lensa dan pelbagai alat-alat optik, melukiskan fungsi mata dan pelbagai kelainan-kelainannya serta menggambarkan teori cahaya yang hakekatnya versi pemula dari teori gelombang yang belakangan dirumuskan oleh Christiaan Huygens. Tambahan keduanya terdiri dari perbincangan ihwal meteorologi, Descartes membicarakan soal awan, hujan, angin, serta penjelasan yang tepat mengenai pelangi. Dia mengeluarkan sanggahan terhadap pendapat bahwa panas terdiri dari cairan yang tak tampak oleh mata, dan dengan tepat dia menyimpulkan bahwa panas adalah suatu bentuk dari gerakan intern. (Tetapi, pendapat ini telah ditemukan lebih dulu oleh Francis Bacon dan orang-orang lain). Tambahan ketiga Geometri, dia mempersembahkan sumbangan yang paling penting dari kesemua yang disebut di atas, yaitu penemuannya tentang geometri analitis. Ini merupakan langkah kemajuan besar di bidang matematika, dan menyediakan jalan buat Newton menemukan Kalkulus. 

Mungkin, bagian paling menarik dari filosofi Descartes adalah caranya dia memulai sesuatu. Meneliti sejumlah besar pendapat-pendapat yang keliru yang umumnya sudah disepakati orang, Descartes berkesimpulan untuk mencari kebenaran sejati dia mesti mulai melakukan langkah yang polos dan jernih. Untuk itu, dia mulai dengan cara meragukan apa saja, apa saja yang dikatakan gurunya. Meragukan kepercayaan meragukan pendapat yang sudah berlaku, meragukan eksistensi alam di luar dunia, bahkan meragukan eksistensinya sendiri. Pokoknya, meragukan segala-galanya. 

Ini keruan saja membuat dia menghadapi masalah yang menghadang: apakah mungkin mengatasi pemecahan atas keraguan yang begitu universal, dan apakah mungkin menemukan pengetahuan yang bisa dipercaya mengenai segala-galanya? Tetapi, lewat alasan-alasan metafisika yang cerdik, dia mampu memuaskan dirinya sendiri bahwa dia sebenarnya "ada" ("Saya berpikir, karena itu saya ada"), dan Tuhan itu ada serta alam di luar dunia pun ada. Ini merupakan langkah pertama dari teori Descartes. 

Makna penting teori Descartes punya nilai ganda. Pertama, dia meletakkan pusat sistem filosofinya persoalan epistomologis yang fundamental, "Apakah asal-muasalnya pengetahuan manusia itu?" para filosof terdahulu sudah mencoba melukiskan gambaran dunia. Descartes mengajar kita bahwa pertanyaan macam itu tidak bisa memberi jawab yang memuaskan kecuali bila dikaitkan dengan pertanyaan "Bagaimana saya tahu?" 

Kedua, Descartes menganjurkan kita harus berangkat bukan dengan kepercayaan, melainkan dengan keraguan. (Ini merupakan kebalikan sepenuhnya dari sikap St. Augustine, dan umumnya teolog abad tengah bahwa kepercayaan harus didahulukan). Memang benar Descartes kemudian meneruskan dan sampai pada kesimpulan teologis yang ortodoks, tetapi para pembacanya lebih tertarik dan menaruh perhatian lebih besar kepada metode yang dikembangkannya ketimbang kongklusi yang ditariknya. (Ketakutan gereja bahwa tulisan-tulisan Descartes akhirnya akan menjadi bahaya, jelas sekali). 

Dalam filosofinya, Descartes menekankan beda nyata antara pikiran dan obyek material, dan dalam hubungan ini dia membela dualisme. Perbedaan ini telah dibuat sebelumnya, tetapi tulisan-tulisan Descartes menggalakkan perbincangan filosofis tentang masalah itu. Permasalahan yang dikemukakannya menarik para filosof sejak itu dan tetap tak terpecahkan. 

Pengaruh besar lain dari konsepsi Descartes adalah tentang fisik alam semesta. Dia yakin, seluruh alam --kecuali Tuhan dan jiwa manusia-- bekerja secara mekanis, dan karena itu semua peristiwa alami dapat dijelaskan secara dan dari sebab-musabab mekanis. Atas dasar ini dia menolak anggapan-anggapan astrologi, magis dan lain-lain ketahayulan. Berarti, dia pun menolak semua penjelasan kejadian secara teleologis. (Yakni, dia mencari sebab-sebab mekanis secara langsung dan menolak anggapan bahwa kejadian itu terjadi untuk sesuatu tujuan final yang jauh). Dari pandangan Descartes semua makhluk pada hakekatnya merupakan mesin yang ruwet, dan tubuh manusia pun tunduk pada hukum mekanis yang biasa. Pendapat ini sejak saat itu menjadi salah satu ide fundamental fisiologi modern. 

Descartes menggandrungi penyelidikan ilmiah dan dia percaya bahwa penggunaan praktisnya dapat bermanfaat bagi masyarakat. Dia pikir, para ilmuwan harus menjauhi pendapat-pendapat yang semu dan harus berusaha menjabarkan dunia secara matematis. Semua ini kedengarannya modern. Tetapi, Descartes, melalui pengamatannya sendiri tak pernah bersungguh-sungguh menekankan arti penting ruwetnya percobaan-percobaan metode ilmiah. 

Filosof Inggris yang masyhur, Francis Bacon, telah menyatakan perlunya penyelidikan ilmiah dan keuntungan yang bisa diharapkan dari sana beberapa tahun sebelum Descartes. Dan argumen yang terkenal Descartes yang berbunyi "saya berfikir, karena itu saya ada," bukanlah pendapatnya yang orisinal. Itu sudah pernah dikemukakan lebih dari 1200 tahun sebelumnya (walau dalam kalimat yang berbeda tentu saja) oleh St. Augustine. Hal serupa juga mengenai "pembuktian" Descartes tentang adanya Tuhan hanyalah variasi dari pendapat ontologis yang pertama kali diucapkan oleh St. Anselm (1033-1109). 

Di tahun 1641 Descartes menerbitkan bukunya yang masyhur Meditations. Dan bukunya Principles of philosophy muncul tahun 1644. Ke dua buku itu aslinya ditulis dalam bahasa Latin dan terjemahan Perancisnya terbit tahun 1647. 

Meskipun Descartes seorang penulis yang lincah dengan gaya prosanya yang manis, nada tulisannya terasa kuno. Betul-betul dia tampak (mungkin akibat pendekatannya yang rasional, dia seperti cendikiawan abad tengah. Sebaliknya Francis Bacon, walau dilahirkan tiga puluh lima tahun sebelum Descartes, nada tulisannya modern). 

Tergambar jelas dalam tulisan-tulisannya, Descartes seorang yang teguh kepercayaannya tentang adanya Tuhan. Dia menganggap dirinya seorang Katolik yang patuh; tetapi gereja Katolik tidak menyukai pandangan-pandangannya, dan hasil karyanya digolongkan ke dalam "index" buku-buku yang terlarang dibaca. Bahkan di kalangan Protestan Negeri Belanda (waktu itu mungkin negeri yang paling toleran di Eropa), Descartes dituduh seorang atheist dan menghadapi kesulitan dengan penguasa. 

Tahun 1649 Descartes menerima tawaran bantuan keuangan yang lumayan dari Ratu Christina, Swedia, agar datang ke negerinya dan menjadi guru pribadinya. Descartes amat kecewa ketika dia tahu sang Ratu ingin diajar pada jam lima pagi! Dia khawatir udara pagi yang dingin bisa membikinnya mati. Dan ternyata betul: dia kena pneumonia, meninggal bulan Februari 1650, cuma empat bulan sesudah sampai di Swedia. 

Descartes tak pernah kawin, tetapi punya seorang anak perempuan yang sayang mati muda. 

Filosofi Descartes dikritik pedas oleh banyak filosof sejamannya, sebagian karena mereka anggap filosofi itu menggunakan alasan yang berputar-putar. Sebagian lagi menunjukkan kekurangan-kekurangan dalam sistemnya. Dan sedikit sekali orang saat ini yang membelanya dengan sepenuh hati. Tetapi, arti penting seorang filosof tidaklah terletak pada kebenaran sistemnya; melainkan pada apakah penting tidaknya ide-idenya, atau apakah ide-idenya ditiru orang dan berpengaruh luas. Dari ukuran ini, sedikitlah keraguan bahwa Descartes memang seorang tokoh yang penting. 

Sedikitnya ada lima ide Descartes yang punya pengaruh penting terhadap jalan pikiran Eropa: (a) pandangan mekanisnya mengenai alam semesta; (b) sikapnya yang positif terhadap penjajagan ilmiah; (c) tekanan yang, diletakkannya pada penggunaan matematika dalam ilmu pengetahuan; (d) pembelaannya terhadap dasar awal sikap skeptis; dan (e) penitikpusatan perhatian terhadap epistemologi. 

Menyimpulkan arti penting keseluruhan Descartes, saya juga mempertimbangkan penemuan ilmiahnya yang mengesankan, khusus penemuannya tentang geometri analitis. Faktor inilah yang saya jadikan alasan menempatkan Descartes dalam urutan agak lebih tinggi daripada filosof-filosof kenamaan seperti Voltaire, Rousseau, dan Francis Bacon.

3.DEFINISI

Persamaan Lingkaran adalah tempat kedudukan titik-titik (x,y) yang berjarak sama terhadap satu titik tertentu.
Persamaan umum lingkaran adalah:

${\displaystyle {\boldsymbol {(}}x-x_{p})^{2}+(y-y_{p})^{2}=r^{2}}$

Mencari jarak antara 2 titik A (x₁,y₁) dan B (x₂,y₂):

${\displaystyle r={\sqrt {(x_{1}-x_{2})^{2}+(y_{2}-y_{1})^{2}}}}$

Mencari jarak antara titik A (x₁,y₁) dan garis Ax+By+C=0 :

${\displaystyle d=\left\vert {\frac {Ax_{1}+By_{1}+C}{\sqrt {A^{2}+B^{2}}}}\right\vert }$

Mencari jari-jari (r) jika diketahui persamaan lingkaran ${\displaystyle x^{2}+y^{2}+Ax+By+C=0}$:

${\displaystyle r={\sqrt {{\frac {1}{4}}A^{2}+{\frac {1}{4}}B^{2}-C}}}$

  4.RUMUS DAN TURUNANNYA

a). Persamaan lingkaran yang berpusat di titik O(0,0) dan berjari-jari “r”

Gambar 1

Perhatikan segitiga OTU pada gambar 1. Titik T(x,y) berada pada lingkaran yang berpusat pada titik O(0,0) maka berlaku OT merupakan jari-jari lingkaran. Selain itu diketahui pula bahwa panjang OU = x dan panjang TU = y . Untuk mendapatkan persamaan lingkaran pada gambar diatas, karena segitiga OUT adalah segitiga siku-siku,maka kita menggunakan teorema pythagoras yaitu sebagai berikut :

Jadi, persamaan lingkaran yang berpusat di titik O(0,0) adalah :

b).Persamaan lingkaran yang berpusat di titik P(a,b) dan berjari-jari “r”

Diketahui sebuah lingkaran yang berpusat dititik T(a,b) dan titik P (x,y) berada pada lingkaran, maka garis TP adalah jari-jari dari lingkaran tersebut.kemudian perhatikan segitiga TPQ siku-siku di Q, pada segitiga TPQ kita dapat mengetahui dengan jelas bahwa panjang TQ = x – a dan PQ = y – b. selanjutnya, dengan menggunakan teorema pythagoras maka dapat di tentukan rumus persamaan lingkaran, sebagai berikut :

Jadi, persamaan lingkaran yang berpusat di titik T(a,b) adalah  :

   

c).   Bentuk umum persamaan lingkaran

Diatas kita telah mengetahui bahwa persamaan lingkaran yang berpusat di titik T(a,b) adalah :

 . jika persamaan lingkaran tersebut diuraikan maka akan dihasilkan persamaan umum lingkaran. Uraiannya sebagai berikut :

Jadi, bentuk umum persamaan lingkaran adalah 

 dengan pusat lingkaran adalah :

dan jari-jari lingkaran adalah :

 Pusat lingkaran dan rumus jari-jari lingkaran diatas diperoleh dengan menjadikan bentuk umum persamaan lingkaran kedalam bentuk kuadrat sempurna. Untuk lebih jelasnya pehatikan uraian berikut :

Karena jika persamaan lingkarannya adalah  maka lingkaran tersebut berpusat di titik (a,b) . jadi , apabila persamaan lingkarannya adalah :

maka pusatnya menjadi :

 
dengan

5.APLIKASI DALAM KEHIDUPAN SEHARI-HARI

Suatu stasiun radio berada pada koordinat (7,3) dalam km. Jika stasiun radio tersebut mempunyai jangkauan gelombang radio sejauh 100 km, maka tentukan persamaan gelombang radio!

Pembahasan:
Soal jenis ini termasuk pada soal lingkaran. Jika kita gambarkan kira kira sketsanya akan jadi,

Karena jangkauan frekuensi 100 km, artinya dari stasiun radio jangkauan frekuensi tersebut 100 km ke segala arah. Ini akan membuat wilayah berupa lingkaran. Sementara pusat stasiun radio (7,3). Maka, persamaan frekuensi tersebut berupa persamaan lingkaran yang berpusat di (7,3) dengan radius 100 km.

Persamaan umum lingkaran:
(x−xp)2+(y−yp)2=r2

Jika di gunakan data di atas akan diperoleh,
(x−7)2+(y−3)2=1002x2+y2−14x−6y−42=0
Jadi persamaan frekuensi radio tersebut,
       x2+y2−14x−6y−42=0.